2011
Analyzing Properties of the C. Elegans Neural Network: Mathematically Modeling a Biological System

Contributors
Tyler Reese, Dylan Yott, Antoni Brzoska, and Daniel Kelleher
Overview
The brain is one of the most studied and highly complex systems in the biological world. This group analyzed the brain of the nematode Caenorhabditis elegans. They used eigenvalues and eigenvectors of the Laplacian matrix — a matrix representation — of the neural network of the nematode brain with an eye on indicators of self-similarity.
The following is a list of the programs this group used in their research. Most of them were written in Matlab.
Publications
The Strichartz Hexacarpet and Higher Dimensional Analogues

Contributors
Matt Begue, Dan Kelleher, Gabe Khan, and Diwakar Raisingh
Overview
The Strichartz hexacarpet is a fractal which can be obtained by repeated barycentric subdivisions of a triangle. This group examined properties of graph approximations and looked at analogous fractals obtained by subdivisions of higher dimensional triangles — n-simplexes. They studied properties of random walks on these fractals, obtaining heat kernel estimates and resistance factors. See also Random Walks on Barycentric Subdivisions and the Strichartz Hexacarpet Experiment. Math. Volume 21, Issue 4 (2012), 402-417.
Presentation
Random Walks on Barycentric Subdivisions and the Strichartz Hexacarpet
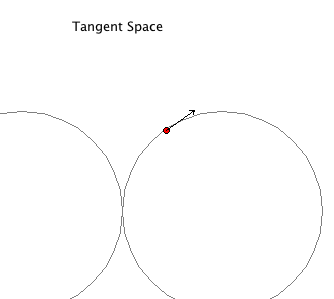
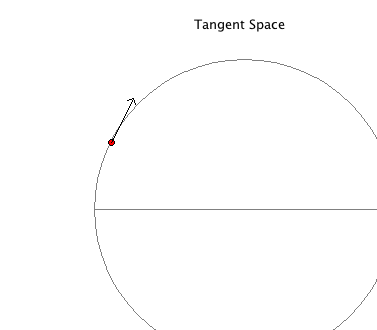
Tangent Space Visualization
Overview
Even in low dimensional examples, basic object in differential geometry, such has tangent spaces and bundles, can only be perceived in at least 4-dimensions. This makes intuitive understanding of these objects difficult. This group created some tools for understanding these objects a little better.
In these “tangent space visualisers,” we explore the concept of tangent vectors and tangent spaces. Below we have two examples, the figure-8 space (left) and the “theta” space (right). Click on the images to download the applets. The arrows indicate the tangent vectors which span the tangent space at any given point, click on any point in the space to move the arrow.